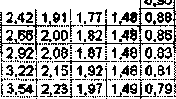|
1. Исследование физических моделей. 2. Моделирование геометрических операций. 3. Биологические модели развития популяций. 4. Моделирование случайных процессов.
Исследование физических моделей. Движение под действием силы тяжести хорошо известны. Это и падение тела с некоторой высоты, и движение тела, брошенного под углом к горизонту, и т.д. Если в таких задачах не учитывать силу сопротивления воздуха, то все перечисленные виды движения описываются известными формулами. Но задачи, в которых сопротивление воздуха учитываются, не менее интересны. ЗАДАЧА Движение парашютиста. I этап. Постановка задачи ОПИСАНИЕ ЗАДАЧИ Парашютист при падении к земле испытывает действие
силы тяжести и силы сопротивления воздуха. Экспериментально установлено, что
сила сопротивления зависит от скорости движения: чем больше скорость, тем больше
сила. При движении в воздухе эта сила пропорциональна квадрату скорости с
некоторым коэффициентом сопротивления k, который зависит от конструкции
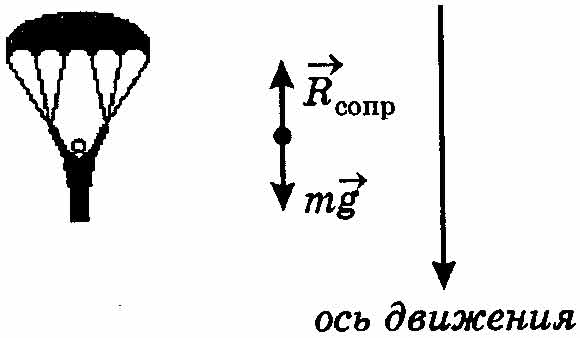
парашюта и веса человека Определите цели моделирования и проведите формализацию задачи. II этап. Разработка модели ИНФОРМАЦИОННАЯ МОДЕЛЬ Составьте информационную модель самостоятельно. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ На рисунке указаны силы, действующие на парашютиста.
Согласно второму закону Ньютона движение под действием сил можно записать
равенством
Получим формулу для вычисления ускорения
Будем рассчитывать скорость и расстояние, которое пролетел парашютист через равные промежутки времени Δt. Формула для вычисления моментов времени имеет вид: ti+1=ti+Δt
Будем также считать, что на каждом промежутке ускорение постоянно и равно аi. Формула для вычисления ускорения имеет вид
где Vi— скорость в начале промежутка (V0 — начальная скорость). Скорость в конце промежутка (и, соответственно, в начале следующего) вычисляется по формуле равноускоренного движения
Расстояние, которое пролетел парашютист, равно сумме
расстояния, пройденного к началу очередного промежутка времени и расстояния,
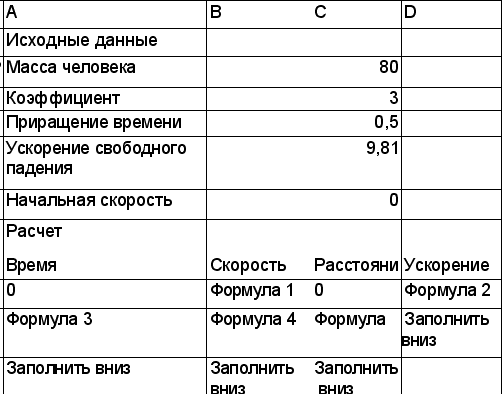
пройденного на этом промежутке КОМПЬЮТЕРНАЯ МОДЕЛЬ Для моделирования выберем среду электронной таблицы. В этой среде информационная и математическая модель объединяются в таблицу, которая содержит три области: исходные данные; промежуточные расчеты; результаты. 1. Заполните область исходных данных. 2. Заполните расчетные столбцы А, В, С, D, в которых вычисляются параметры движения парашютиста:
3.Введите формулы в расчетные ячейки. Пример заполнения расчетной таблицыЯчейка Формула А9 0 (начальный момент времени) В9 =$С$6 С9 0 (расстояние в начальный момент) D9 =$С$5-$С$3*В9^2/$С$2 А10 =А9+$С$4 В10 =В9+D9*$С$4 С10 =С9+В9*$С$4+D9*$С$4^2/2 III этап. Компьютерный эксперимент
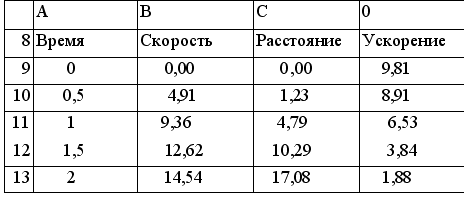
ПЛАН ЭКСПЕРИМЕНТА ТЕСТИРОВАНИЕ Провести тестовый расчет компьютерной модели по данным, приведенным в таблице. ЭКСПЕРИМЕНТ 1 Исследовать движение тела под действием силы тяжести и сопротивления воздуха. ЭКСПЕРИМЕНТ 2 Подобрать значение коэффициента сопротивления и для безопасного приземления парашютиста. ЭКСПЕРИМЕНТ 3 Исследовать зависимость скорости, ускорения от начальной скорости движения. ЭКСПЕРИМЕНТ 4 Исследовать, как изменяется расстояние полета до стабилизации скорости падения. ПРОВЕДЕНИЕ ИССЛЕДОВАНИЯ ТЕСТИРОВАНИЕ 1. Сравните результаты тестового расчета с результатами, приведенными в примере расчета. Пример тестового расчета
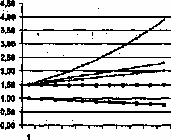
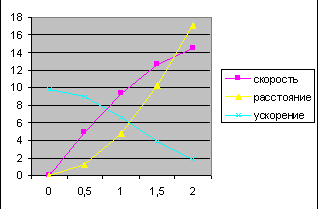
2. Постройте диаграмму изменения скорости, ускорения и расстояния в зависимости от времени.
Диаграмма изменения скорости, ускорения и расстояния в зависимости от времени. ЭКСПЕРИМЕНТ 1. Исследование движения тела с учетом сопротивления воздуха Определите по диаграмме и по таблице, как изменяется с течением времени скорость движения парашютиста. Через сколько секунд наступает стабилизация скорости падения? Определите по диаграмме и по таблице, как изменяется с течением времени ускорение парашютиста. Определите по диаграмме и по таблице, какое расстояние пролетит парашютист до стабилизации скорости движения. Результаты поместите на свободном поле в электронной таблице. Измените шаг времени (0,1 с) и определите скорость стабилизации движения, расстояние полета до стабилизации. Результаты исследования приведите в таблице. ЭКСПЕРИМЕНТ 2. Подбор коэффициента сопротивления Изменяя значение коэффициента А (ячейка СЗ), подберите скорость стабилизации движения, безопасную для приземления тренированного человека (8 м/с). ЭКСПЕРИМЕНТ 3. Исследование стабилизации скорости и расстояния в зависимости от начальной скорости Парашютист, выпрыгнув из самолета, некоторое время летит в свободном падении, набирает достаточно большую скорость движения и только потом раскрывает парашют. Измените значение начальной скорости (10 м/с). По таблице расчетов определите, как изменится: начальное ускорение скорость стабилизации расстояние полета до стабилизации скорости. 3. Результаты эксперимента запишите на свободном поле электронной таблицы. Сделайте вывод. Результаты эксперимента 3
Примечание.Обратите внимание, как изменяется начальное ускорение. Учтите, что оно не может быть большим, так как ускорение 3g (30 м/с2) вызывает очень большие перегрузки. IV этап. Анализ результатов моделирования По результатам компьютерного эксперимента ответить на следующие вопросы: Как изменяется скорость парашютиста с течением времени? Как изменяется скорость парашютиста при изменении коэффициента сопротивления? Каким должен быть коэффициент сопротивления, чтобы парашютист опустился на землю со скоростью 8 м/с? Как изменяется скорость движения и как зависит установившаяся скорость равномерного движения парашютиста от начальной скорости? Через сколько секунд после начала движения скорость парашютиста можно считать установившейся? На какой высоте от земли парашютист должен раскрыть парашют, чтобы приземлиться с заданной скоростью. |
||||||||
|
Моделирование геометрических операций. I этап. Постановка задачи ОПИСАНИЕ ЗАДАЧИ Вся история геометрии связана с практикой построений при помощи подручных средств для измерения недоступного. В Древнем Египте, задолго до доказательства Пифагором его знаменитой теоремы, использовали треугольник со сторонами, соотносящимися как 3:4:5, для получения прямых углов в строительстве. Фалесу Милетскому, жившему в VI в. до н. э., приписывается метод измерения расстояния до кораблей, находящихся в море, с использованием признаков подобия треугольников. К задачам, поставленным еще в древности, относятся задачи деления отрезков и углов на две равные части. Их решение было известно еще в догреческий период (V в. до н. э.). Построения в графическом редакторе и на листе бумаги несколько
отличаются, потому что компьютерные инструменты не совсем идентичны привычным,
повседневным.
ЦЕЛЬ МОДЕЛИРОВАНИЯ При отсутствии специальных инструментов (линейки, транспортира, циркуля) смоделировать основные геометрические операции.
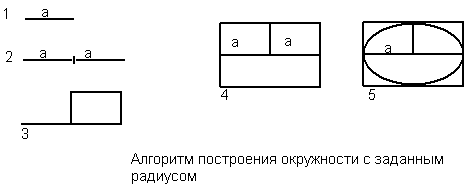
ФОРМАЛИЗАЦИЯ ЗАДАЧИИ сходные геометрические объекты (отрезок, радиус, угол) задаются в левом верхнем углу рабочего поля. Для построений используются их копии. Построение основывается на законах геометрии. IРазработка модели МОДЕЛЬ 1. Деление отрезков (моделирование функций линейки) Алгоритм деления
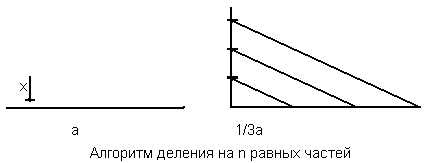
отрезка пополам приведен на рисунке Построение основано на том, что высота в равнобедренном треугольнике является одновременно биссектрисой и медианой. Для построения достаточно инструмента Линия и клавиши Shift. Алгоритм деления отрезка на п равных частей (для га=3)
приведен на рисунке Для выполнения операции деления используется отрезок произвольной длины х. Построение основано наподобие треугольников. Параллельность линий достигается копированием.
МОДЕЛЬ 2. Построение окружности заданного радиуса и определение ее центра (моделирование функций циркуля) Окружность в графическом редакторе вписывается в квадрат со
стороной, равной удвоенному радиусу. Алгоритм построения окружности изображен на
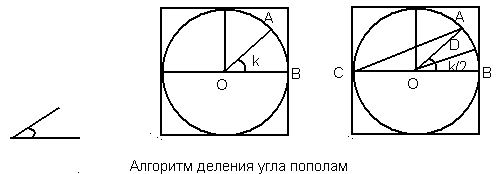
рисунке МОДЕЛЬ 3. Деление угла пополам (моделирование функции транспортира) На рисунке 1.4 приведен один из вариантов алгоритма деления
В качестве дополнительного построения используется окружность любого радиуса. В ее центр помещается копия угла, подлежащего делению. Углы АОВ и АСВ относятся как 2:1 (докажите это). Отсюда, если линия ВО параллельна линии АС, то она является биссектрисой заданного угла. Построение сводится к копированию части отрезка АС и установке его копии к точке О. Полученная параллельная линия DО разделит заданный угол пополам.
III этап. Компьютерный эксперимент ПЛАН ЭКСПЕРИМЕНТА
|
|
В биологии при исследовании развития биосистем строятся динамические модели изменения численности популяций различных живых существ (бактерий, рыб, животных и пр.) с учетом различных факторов. Взаимовлияние популяций рассматривается в моделях типа «хищник-жертва». Формальная модель. Изучение динамики численности популяций естественно начать с простейшей модели неограниченного роста, в которой численность популяции ежегодно увеличивается на определенный процент. Математическую модель можно зависать с помощью рекуррентной формулы, связывающей численность популяции следующего года с численностью популяции текущего года, с использованием коэффициента роста а: Xn+1=a · xn
Например, если ежегодный прирост численности популяции составляет 5%, то а = 1,05. В модели ограниченного роста учитывается эффект перенаселенности, связанный с нехваткой питания, болезнями и так далее, который замедляет рост популяции с увеличением ее численности. Введем коэффициент перенаселенности b, значение которого обычно существенно меньше а (b<<a). Тогда коэффициент ежегодного увеличения численности равен (а - b • хп) и формула принимает вид:
xn+1=(а - b • хп ) • хп. В модели ограниченного роста с отловом учитывается, что на численность популяций промысловых животных и рыб оказывает влияние величина ежегодного отлова. Если величина ежегодного отлова равна с, то формула принимает вид:
xn+1=(а - b • хп ) • хп - c. Популяции обычно существуют не изолированно, а во взаимодействии с другими популяциями. Наиболее важным типом такого взаимодействия является взаимодействие между жертвами и хищниками (например, караси-щуки, зайцы-волки и так далее). В модели «хищник-жертва» количество жертв хп и количество хищников уп связаны между собой. Количество встреч жертв с хищниками можно считать пропорциональным произведению количеств жертв и хищников, а коэффициент f характеризует возможность гибели жертвы при встрече с хищниками. В этом случае численность популяции жертв ежегодно уменьшается на величину f • хп • уп и формула для расчета численности жертв принимает вид:
xn+1=(а
- b • хп
) • хп
– c - f • хп • уп.Численность популяции хищников в отсутствие жертв (в связи с
отсутствием пищи) уменьшается, что можно описать рекуррентной формулой
yn+1= d•yn где значение коэффициента а < 1 характеризует скорость
уменьшения численности популяции хищников. Увеличение популяции хищников можно считать пропорциональной
произведению собственно количеств жертв и хищников, а коэффициент е
характеризует величину роста численности хищников за счет жертв. Тогда для
численности хищников можно использовать формулу:
yn+1= d•yn + e• хп • уп Компьютерная модель. Построим в электронных таблицах компьютерную
модель, позволяющую исследовать численность популяций с использованием различных
моделей: неограниченного роста, ограниченного роста, ограниченного роста с
отловом и «хищник-жертва».
Рост численности популяций 1. В ячейки
В1 и В6 внести начальные значения численности популяций жертв и хищников. В ячейки В2:В5 внести значения коэффициентов а, Ь, с и
f, влияющих на изменение численности жертв. В ячейки В 7 и В8 внести
значения коэффициентов d и е, влияющих на изменение численности
хищников. В столбце D будем вычислять численность популяции в соответствии с
моделью неограниченного роста, в столбце Е — ограниченного роста, в столбце F —
ограниченного роста с отловом, в столбцах G и Н — «хищник-жертва». 2. В ячейки
D1, Е1, F1и G1 внести значения начальной численности популяций жертв, в ячейку
Н1 — хищников. В ячейку D2 внести рекуррентную формулу неограниченного роста
=$В$2*D1. В ячейку Е2
внести рекуррентную формулу ограниченного роста =($В$2-$В$3*Е1)*Е1. В ячейку F2
внести рекуррентную формулу ограниченного роста с отловом
=($В$2-$В$3*F1)*F1-$В$4. В ячейку G2
внести рекуррентную формулу изменения количества жертв =($В$2-$В$3*G1)*G1-$В$4-$В$5*G1*Н1.
В ячейку Н2 внести рекуррентную формулу изменения количества хищников
=$В$7*Н1+$В$8*(G1*Н1). 3.
Скопировать внесенные формулы в ячейки столбцов командой [Правка – Заполнить -
Вниз]. Для
визуализации компьютерной модели построим графики изменения популяций с течением
времени. 4. Выделить столбцы данных и построить диаграмму типа График.
Появятся графики изменения численности популяций в соответствии с моделями
неограниченного роста, ограниченного роста, ограниченного роста с отловом,
моделью хищник-жертва. Исследование модели. Изменяя значения начальных численностей
популяций, а также коэффициенты, можно получать различные варианты изменения
численности популяций в зависимости от времени. Практические
задания Исследовать
модель развития популяций и определить, через сколько лет произойдет удвоение
численности популяции в модели неограниченного роста. В модели
ограниченного роста с отловом установить предельное значение величины отлова при
заданных значениях коэффициентов а и b. Моделирование случайных процессов. Игра в
рулетку. I этап.
Постановка задачи ОПИСАНИЕ ЗАДАЧИКазино процветают из-за того, что у владельца всегда есть
некоторое преимущество перед игроком. Например, в одном из вариантов рулетки
колесо имеет 38 лунок: 36 пронумерованы и разбиты на черный и красный цвет, а
две оставшиеся имеют № 0 и 00 и выкрашены зеленым. Игрок, ставя на красное или
черное, имеет на выигрыш 18 шансов из 38, а на то, что он проиграет — 20 шансов
из 38. Повторить эксперимент задачи 3.32, считая, что у вас
есть некоторое число фишек и вы хотите увеличить свой капитал в 2 раза. Если
колесо остановилось на выбранной вами цифре, ваш капитал увеличится на величину
ставки, в противном случае ставка уйдет в доход
казино. ЦЕЛЬ МОДЕЛИРОВАНИЯ Моделирование возможных игровых ситуаций и выработка
тактики, чаще приводящей к результату (положительному или
отрицательному). Предостережение излишне азартным игрокам. ФОРМАЛИЗАЦИЯ ЗАДАЧИ Проведем формализацию задачи в виде поиска ответов на
следующие вопросы: Уточняющий вопрос (Ответ) Что моделируется? (Процесс игры)
Каков характер процесса? (Случайный)
Чем определяется выигрыш/проигрыш? (Положением рулетки)
Какие объекты участвуют в процессе? (Игрок, казино и рулетка)
Чем характеризуется игрок? (Начальным капиталом Кнач,
Ставкой СТ, Текущей наличностью
Ктек)
Чем характеризуется рулетка? Положением (красный сектор/зеленый
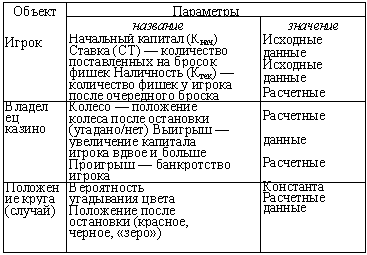
сектор/сектора 0 и 00) II этап. Разработка модели ИНФОРМАЦИОННАЯ МОДЕЛЬ Здесь моделируется игра. Игра — это процесс, в котором участвуют три
объекта: игрок, владелец казино и случай, представленный в данной игре рулеткой.
Случай характеризуется угадыванием или нет того, какой цвет выпал на колесе, и имеет два значения
«угадал» (1) или «не
угадал» (0). Математическая модель процесса складывается из следующих
рассуждений.
Имитировать ставку игрока с помощью функции СЛУЧ_ЧИСЛО() бессмысленно, так как это зависит
только от него. Игрок может ставить всегда на красный цвет, или всегда на
черный, или через раз... Имитировать результат поворота колеса можно с помощью функции
СЛУЧ_ЧИСЛО(), которая выдает числа в диапазоне 0≤ х <1.
Вероятность угадывания цвета составляет по условию
задачи 18/38, что равно 0,47. Число 0,47 делит диапазон случайных чисел на две
неравные части. Попадание в меньшую часть диапазона означает угадывание
результата (у него меньшая вероятность), в большую — неудачу (с большей
вероятностью). Эту ситуацию можно описать следующей формулой: Колесо = ЕСЛИ(СЛУЧ_ЧИСЛО( )<0,47; 1;
0).
КОМПЬЮТЕРНАЯ МОДЕЛЬ Для моделирования выберем среду электронной таблицы. В этой
среде информационная и математическая модель объединяются в таблицу, которая
содержит три области: исходные данные; расчетные данные (результаты); статистика по экспериментам. Ввести в таблицу исходные данные: Ввести в расчетную часть следующие формулы: Ячейка Формула ~- А7 =ЕСЛИ(СЛУЧ_ЧИСЛО()<0,47; 1; 0) (1) B7 =ЕСЛИ(А7=1; $В$4+$D$4; $В$4-$D$4) (2) С7 =ЕСЛИ(В7<2*$В$4; "-"; "банк") (3) D7 =ЕСЛИ(В7>0;"-"; "банкрот") (4) B8 =ЕСЛИ(А8=1; В7+$D$4; В7-$D$4)
(5)
II этап. Компьютерный
эксперимент ПЛАН
ЭКСПЕРИМЕНТА
ТЕСТИРОВАНИЕ
Проверить правильность ввода формул.
ЭКСПЕРИМЕНТ 1
Исследовать выпадение выигрыша в течение одного сеанса игры.
ЭКСПЕРИМЕНТ 2 Собрать статистические данные о
выигрыше и проигрыше в течение нескольких сеансов игры с различными значениями
ставок и исследовать
их.
ПРОВЕДЕНИЕ ИССЛЕДОВАНИЯ
ТЕСТИРОВАНИЕ Введите в таблицу
контрольные исходные данные и расчетные формулы в первую строку. Результаты
сравните с приведенными в таблице. Если в столбце Колесо результат получился
равным 1, данные в остальных столбцах должны быть следующими: Видим увеличение наличности
на величину ставки. Если в столбце Колесо результат получился равным 1, данные в
остальных столбцах должны быть следующими: Видим уменьшение наличности на величину ставки. ЭКСПЕРИМЕНТ 1. Имитация одного сеанса игры для определенной
ставки 1. Скопируйте формулы в нижестоящие ячейки в обозримом
пространстве экрана (примерно 20 поворотов колеса). Таким образом вы моделируете
сразу весь сеанс игры.
Появление в столбце Выигрыш сообщения «банк» означает удвоение
наличности, а в столбце Проигрыш сообщения «банкрот» — нулевую наличность. И то
и другое приводит к концу сеанса игры. Нижестоящие результаты игнорируются.
Сеанс игры считается законченным. 2.Следующий сеанс игры проведите в тех же ячейках путем обновления
данных 1-го столбца, для чего столбец следует выделить и выбрать команду
Заполнить вниз в меню Правка. 3.Соберите статистику игры. Для этого в свободной области таблицы
запишите результаты 10—20 сеансов игры в следующем
виде: По собранной статистике ответьте на вопросы: Кто чаще выигрывает — казино или игрок? Сколько в среднем поворотов
колеса надо сделать до окончания игры? ЭКСПЕРИМЕНТ 2. Набор статистики для самостоятельно выбранной
ставки Измените размер ставки (4, 7 или 10 монет). Сделайте 20 поворотов колеса. Игра может закончиться раньше, Проведите 10 сеансов игры для каждой ставки. Соберите статистику игры. Для этого в свободной области электронной
таблицы запишите результаты 10 сеансов игры в следующем
виде: В
столбце Результат возможны следующие значения: выигрыш (при появлении значения «банк»);проигрыш (при появлении значения «банкрот»); нет (нерезультативная игра). IV этап. Анализ результатов Проанализировать данные области «Статистика». Сравнить количество
выигрышей и проигрышей. Просуммировать столбцы выигрышей и проигрышей и сделать
выводы. Исследование математических моделей Исследование математических моделей начинается с записи
формальной модели на языке определенной области математики: алгебры, геометрии
и так далее. Приближенное решение уравнений На языке алгебры формальные модели записываются с
помощью уравнений, точное решение которых основывается на поиске равносильных
преобразований алгебраических выражений, позволяющих выразить переменную
величину с помощью формулы. Точные решения существуют только для некоторых
уравнений определенного вида (линейные, квадратные, тригонометрические и др.),
поэтому для большинства уравнений приходится использовать методы приближенного
решения с заданной точностью (графические, числовые и др.). Графический метод. Построение графиков функций может
использоваться для грубо приближенного решения уравнений. Для не имеющего
точного алгебраического решения уравнения вида f(x) = О, где f(x) — некоторая непрерывная функция, корень (или корни)
этого уравнения является точкой (или точками) пересечения графика функции с
осью ОХ. Задача. Найти графическим методом корень уравнения я3
- cosjc = 0,
которое не имеет точного алгебраического решения. Проект
«Приближенное «т. решение уравнения» 1. В программный код проекта «Построение графика
функции» в цикл построения графика ввести строку: picGraph.PSet
(sngX, sngX л 3 - Cos(sngX)) График функции пересекает ось ОХ один раз, и,
следовательно, уравнение имеет один корень. По графику грубо приближенно можно
определить, что х т 0,8. Числовой метод половинного деления. Для решения
уравнений с заданной точностью можно применить разработанные в вычислительной
математике числовые итерационные методы решения уравнений. Если мы знаем
отрезок, на котором существует корень, и функция на краях этого отрезка
принимает значения разных знаков, то можно использовать метод половинного
деления. Идея метода состоит в выборе точности решения и сведении
первоначального отрезка [А;В], на котором существует корень уравнения, к
отрезку заданной точности. Процесс сводится к последовательному делению
отрезков пополам точкой С = (А+В)/2 и отбрасыванию той половины отрезка
([А;С] или [С;В]), на котором корня нет. Выбор нужной половины отрезка основывается на проверке
знаков значений функции на его краях. Выбирается та половина, на которой
произведение значений функции на краях отрицательно, то есть где функция
пересекает ось абсцисс. Процесс продолжается до тех пор, пока длина отрезка не
станет меньше удвоенной точности. Деление этого отрезка пополам дает значение
корня х = (А+В)/2 с заданной точностью. 2.
Поместить на
форму текстовые поля для ввода числовых значений концов отрезка А и В, поле
для ввода точности вычислений и поле для вывода значений корня. 3.
Поместить на
форму кнопку и создать событийную процедуру, вычисляющую корень уравнения
методом половинного деления с использованием цикла с постусловием: Private Sub cmdNum_Click() dblA = Val(txtA.Text) dblB = Val(txtB.Text) dblE = Val(txtE.Text) Do dblC = (dblA + dblB) / 2 If (dblA л 3 - Cos (dblA) )
* (dblC л 3 - Cos (dblC) ) < 0 Then dblB = dblC Else dblA = dblC End If While (dblB - dblA) txtX.Text = (dblA + dblB End Sub Из графика функции видно,
что корень находится на отрезке [0,5;1]. Введем в текстовые поля
значения концов отрезка, а также точность вычислений (например, 0,00001).
В текстовое поле будет выведено значение корня с заданной точностью: х
= 0,86547. Вероятностные модели Вероятностные
модели базируются на использовании больших серий испытаний со случайными
параметрами, причем точность полученных результатов зависит от количества проведенных
опытов. Воспользуемся методом Монте-Карло для приближенного вычисления площадей
геометрических фигур. Качественная
модель метода Монте-Карло. Сначала построим качественную вероятностную
модель данного метода: • поместим
геометрическую фигуру полностью внутрь квадрата; • будем
случайным образом «бросать» точки в этот квадрат, то есть с помощью генератора
случайных чисел задавать точкам координаты внутри квадрата; • будем
считать, что отношение числа точек, попавших внутрь фигуры, к общему числу
точек в квадрате прибли- зительно равно отношению площади фигуры к площади квадрата, причем это отношение тем точнее, чем больше количество точек. Рис. 5.8. Круг, вписанный в квадрат Формальная
модель. Построим формальную модель для вычисления площади круга радиуса R, центр которого
совпадает с началом коорди- нат. Круг
вписан в квадрат со стороной 2R, площадь которого вычисляется как 4R2 (рис. 5.8). Пусть N —
количество точек, которые случайным образом генерируются внутри квадрата.
Случайный выбор координат точек, которые попадают внутрь квадрата (N точек),
должен производиться так, чтобы координаты точек х и у удовлетворяли
условиям: -R < х
< R и
-R < у < R. Пусть М — количество точек, попавших внутрь круга,
то есть их координаты удовлетворяют условию: х2 + у2
< R2.
Тогда площадь круга можно вычислить по формуле: S = 4R2 ¦ M/N. Компьютерная модель.
Разработаем на языке Visual Basic компьютерную модель, позволяющую определять площадь круга
методом Монте-Карло. 3. 1. Поместить
на форму графическое поле, в котором будет отображаться процесс случайной
генерации точек, квадрат, круг и оси координат. 2.
Поместить на форму два текстовых поля для ввода
радиуса окружности и количества генерируемых точек и одно поле для вывода
значения площади круга. Поместить на форму кнопку и создать для нее событийную
процедуру, которая обеспечивает ввод значений радиуса окружности в переменную R, ввод количества генерируемых
точек в переменную N, генерацию
случайных точек, подсчет в переменной М количества точек, попавших внутрь
круга, вычисление и вывод значения площади круга в текстовое поле: |













 Например, графический редактор не имеет линейки, в нем нет инструмента,
подобного транспортиру, в окружности, нарисованной в графическом редакторе, не
определен центр. Поэтому необходимо научиться строить модели геометрических
операций: деление отрезка и угла на равные части, определение центра окружности
и др. Это можно сделать, используя законы геометрии.
Например, графический редактор не имеет линейки, в нем нет инструмента,
подобного транспортиру, в окружности, нарисованной в графическом редакторе, не
определен центр. Поэтому необходимо научиться строить модели геометрических
операций: деление отрезка и угла на равные части, определение центра окружности
и др. Это можно сделать, используя законы геометрии.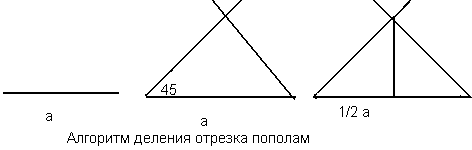
.gif) В ячейках
столбцов ознакомиться с динамикой изменения численности популяции.
В ячейках
столбцов ознакомиться с динамикой изменения численности популяции.